I den här resursen får dina elever undersöka och diskutera vad som är mest sannolikt och varför? Den stora frågan är: Vilken häst kommer att vinna hästkapplöpningen? Resursen består av tre delar och genomförs både individuellt, i par och i helklass.
Missa inte alla samlade dokument som ligger längst ner på sidan.
Del 1: Spelet – vilken häst vinner?
1. Dela in eleverna i par.
2. Visa eleverna GeoGebra applikationen Vilken häst vinner? Förklara hur applikationen fungerar.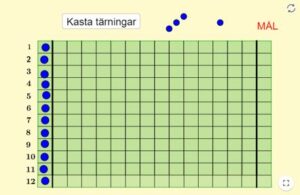
Genom att trycka på knappen, simuleras ett tärningskast med två tärningar. Summan av tärningarnas prickar avgör vilken häst (blå prick) som får flytta fram ett steg på spelplanen. När en häst kommit över mållinjen är spelomgången slut. Innan eleverna börjar spela, ska de ha valt den häst som de tror kommer att gå över mållinjen först.
3. Dela applikationen med eleverna, exempelvis genom att dela länken i Google Classroom.
Uppmana eleverna att behålla spelplanen intakt inför klassdiskussionen. De ska alltså inte nollställa spelet. När alla paren har spelat klart sin första spelomgång, skriv upp de vinnande hästarna på tavlan. Håll därefter en diskussion i helklass utifrån resultatet. Var särskilt uppmärksam på om någon elev har valt häst nummer 1 till vinnarhäst.

4. Samla klassen för att diskutera vad de erfarit och upptäckt under spelets gång. Diskutera i helklass.
Exempel på antaganden eller slutsatser som kan komma fram under klassdiskussionen:
- Alla hästar har inte lika stor chans att vinna
- P(Häst: 1 vinner) = 0
- Häst nummer 6, 7, och/eller 8 verkar ha störst sannolikhet att vinna
- Vilken häst som helst (utom 1) kan vinna – det är slumpen som avgör
- Verkar som om det är lite större sannolikhet för vissa av hästarna
- Det verkar som att häst nr 7 har störst chans att vinna
5. Efter klassdiskussionen låt eleverna göra klart Tabell 2 på elevbladet. Be eleverna att delge hur många tärningskast som krävdes för att genomföra en spelomgång. Räkna tillsammans ut ett genomsnitt över hur många kast som krävs för att genomföra en spelomgång.

6. Låt eleverna skapa ett stolpdiagram över spelomgången i GeoGebra. Låt eleverna ta hjälp av instruktioner från en Lathund i form av en pdf.
Påminn eleverna att ta ett fotografi eller en skärmdump av sin konstruktion i GeoGebra. De kommer att behöva den till del 3.
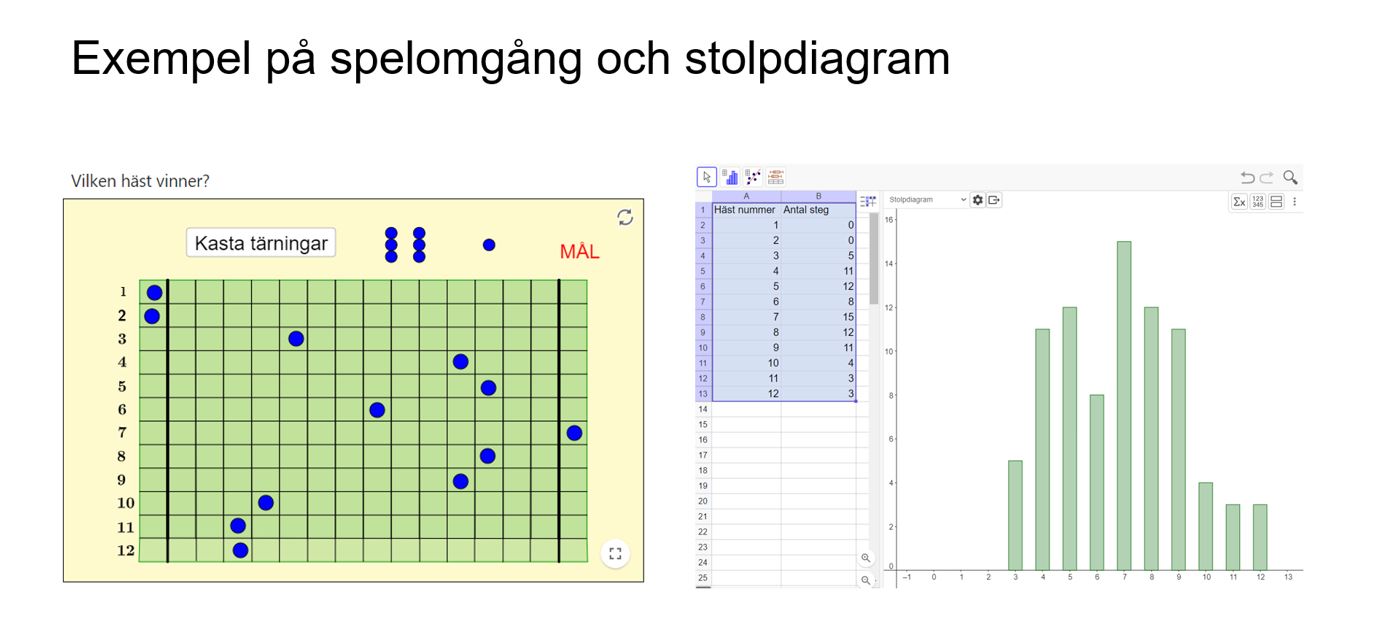
7. Avsluta del1 genom att låta eleverna ta ställning till utifrån diskussionen som varit, samt deras resultat från spelet de gjorde om de valt att byta eller behålla sin häst om de skulle spela spelet en gång till:
Förslag på frågor att ställa:
- Välj ut någon/några elever som valt att byta häst och motivera varför?
- Välj ut någon/några elever som valt att behålla sin häst och motivera varför?
- Vilken häst tror ni har störst chans att vinna?
Led sedan in klassen på nästa del, där de ska undersöka vidare om det kan vara så att häst nummer x har störst chans att vinna tävlingen. Om du väljer att genomföra del 2 nästkommande lektion kan det vara bra att återknyta till det ni gjorde.
Del 2: Undersök vidare
1. Denna del kan genomföras på två olika sätt. Antingen får eleverna använda en färdig applikation, som simulerar 100 tärningskast med två tärningar och visualiserar resultatet i en tabell och stolpdiagram. Besök webbplatsen GeoGebra för att simulera tärningskasten. Det andra alternativet handlar om att eleverna själva får skapa simuleringen i GeoGebra, utifrån det medelvärde ni räknade fram på hur många tärningskast som krävs för att avsluta en spelomgång. Instruktioner för att skapa simuleringen finns i lathunden.
2. Låt eleverna fylla i tabell 3 på elevbladet.

3. Samla eleverna igen för en klassdiskussion.
Klassdiskussion
Låt eleverna skriva upp vinnarhästen respektive spelomgång på tavlan eller i ett digitalt dokument som du projicerar, så att alla kan se.
Öppna filen i ett nytt fönster.
Förhoppningsvis är det nu tydligt att tärningssumman 7 verkar förekomma flest gånger.
Men hur kan vi ta reda på att det är så?
Vilka möjliga utfall finns det när vi slår två tärningar och hur ser kombinationerna ut?
4. Låt eleverna undersöka vilka olika tärningskombinationer som är möjliga och om det är så att det är summan 7 som kan kombineras ihop på flest sätt. Dela gärna ut fysiska tärningar till paren som de kan använda i sin undersökning. Låt eleverna visa på olika sätt exempelvis med stöd av en fyrfältare. Det finns en fyrfältare i elevbladet som ni kan använda er av.

5. Avslutande genomgång:
Eventuellt avsluta med en genomgång över hur man systematiskt kan visa alla utfallen, exempelvis i ett utfallsdiagram. Här blir det tydligt att det är just summan 7 som har flest kombinationer.
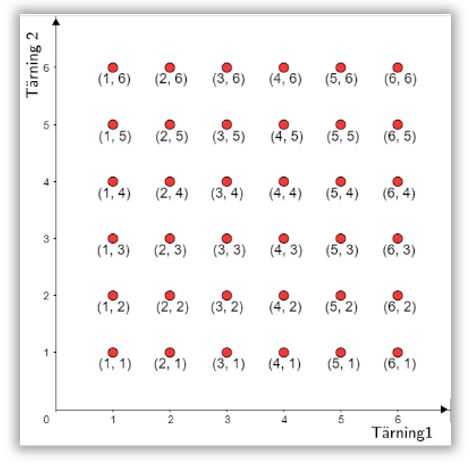
Ge också exempel på andra på situationer som kan visas med hjälp av ett utfallsdiagram. Exempelvis singla slant.
Avsluta med att presentera vilket centralt innehåll och vilka lärandemål eleverna har arbetat med.
Delar av kursplanen Lgr22 som berörs:
Syftestexten:
Genom undervisningen ska eleverna ges förutsättningar att utveckla förtrogenhet med grundläggande matematiska begrepp och metoder och deras användbarhet. Vidare ska eleverna genom undervisningen ges möjligheter att utveckla kunskaper i att använda digitala verktyg och programmering för att kunna undersöka problemställningar och matematiska begrepp, göra beräkningar samt för att presentera och tolka data.
Centralt innehåll:
- Sannolikhet och metoder för att beräkna sannolikheter i olika situationer. Bedömningar av risker och chanser utifrån datorsimuleringar och statistiskt material.
Del 3: Laborationsrapport
Låt eleverna individuellt dokumentera sitt arbete, resultat och slutsatser i en laborationsrapport.
Du visar för närvarande ett platshållarinnehåll från Google Drive. För att komma åt det faktiska innehållet, klicka på knappen nedan. Observera att detta kommer att dela data med tredjepartsleverantörer.
Öppna filen i ett nytt fönster.
Samlade dokument
Lärarhandledning för hela resursen
Elevblad med samtliga elevinstruktioner
Lathund för att göra stolpdiagram i GeoGebra
Öppna filen i ett nytt fönster.
Öppna filen i ett nytt fönster.
Spara som favorit
Du måste logga in för att kunna spara som favorit.

