Problemet består i att en grupp vuxna samt två barn ska ro över en flod. Gummibåten som de har till förfogande kan ta begränsad last (ca 85 kg). Hur ska de på enklaste sätt göra för att ta sig över? Det gäller i första hand för eleverna att hitta ett sätt att få alla över. Därefter utvidgas problemet med bland annat olika antal vuxna.
Lektionsförslag
Inled genom att berätta förutsättningarna för problemet: 7 vuxna (anpassa för yngre elever med lägre antal vuxna) och 2 barn ska ta sig över en flod. Till sin hjälp har de en gummibåt som kan bära antingen en vuxen, eller max två barn åt gången. Plocka fram 9 elever som med hjälp av publiken får dramatisera problemet, hur de tar sig över. (Här kan du använda en rockring som gummibåt, samt två västar/kepsar för att markera barnen samt något för att markera floden). Låt eleverna hålla på tills alla är över. När de lyckats, ställ frågan: Hur många gånger blev det? Sätt eleverna i grupper/par där de får försöka lösa problemet tillsammans.
Här är det fördelaktigt med någon form av laborativt material. Till exempel multilink och centikuber som får symbolisera vuxna respektive barn och en tändsticksask som symboliserar båten. Annat material går så klart också bra.
Låt eleverna göra flera försök med olika antal vuxna för att lättare hitta ett mönster. Om/När gruppen tror att de löst problemet, utmana dem att skriva ner lösningen med hjälp av olika representationer. Dela ut fyrfältaren/tanketavlan.
Matematik i uppgiften:
- Mönster
- Jämna och udda tal
- Tabell
- Diagram
- Formel
- Ekvation
Helklassdiskussion:
Börja med att de olika grupperna får berätta hur många gånger de kom fram till. Skriv upp alla alternativ på tavlan. Fråga om där finns några svar som inte är rimliga? (Alla jämna antal roddturer är orimliga, då roddbåten i så fall är på fel sida. Första och sista turen blir ett udda tal.)
Samla alla data som eleverna kommit fram till. Kanske utgå från en tabell, någon grupp har gjort. Kan ni se något mönster? Utifrån mönstret kan ni formulera en regel? Kan ni utifrån regeln formulera en algebraisk formel?
Lösningsförslag:
Svar: Det tar 29 roddturer för att 7 vuxna och 2 barn ska ta sig över. Det räcker egentligen med 3 turer för att få över 1 vuxen men för att kunna börja om med nästa vuxen måste båten tillbaks till första stranden. Sen krävs det en extra tur för att få över det sista barnet.
Logiskt/språkligt resonemang:
På den första turen ska två barn åka över. Nästa tur ska det ena barnet stanna kvar och det andra ska tillbaks. Den tredje turen ska en vuxen åka över till andra sidan. Den fjärde turen så ska barnet på den sidan åka tillbaka igen. Så fortsätter man tills alla är över.
Alltså blir det 4 turer per vuxen och sen en sista extra tur för barnen därför tar man:
antalet vuxna ∙ 4 +1
Bild:
Tabell
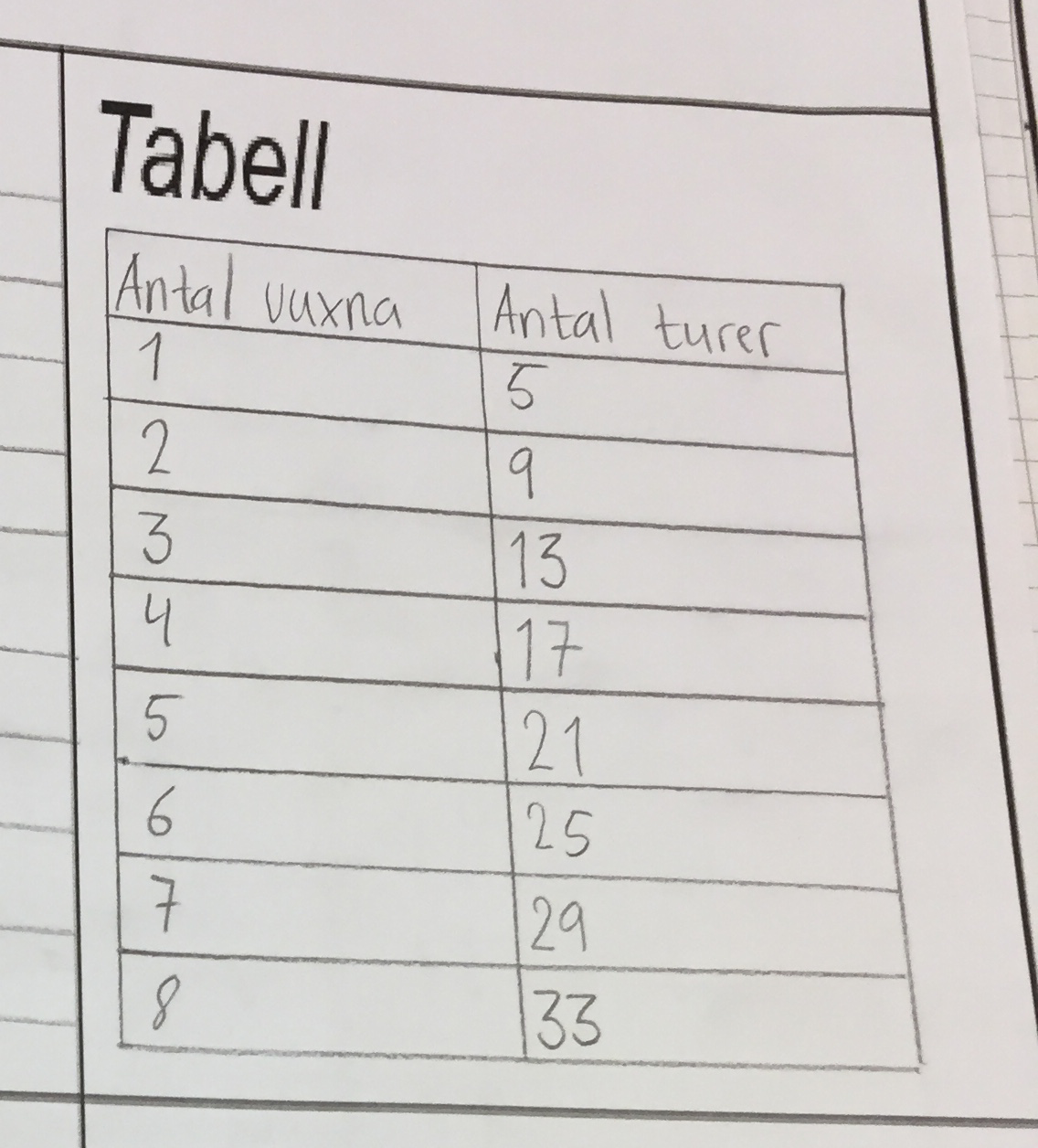
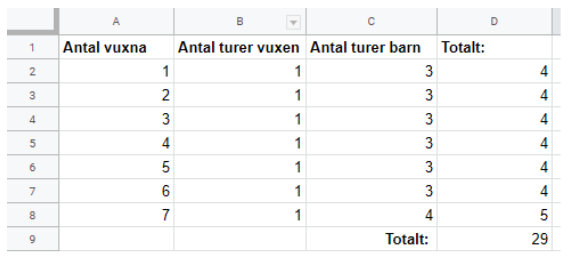
Diagram/graf:
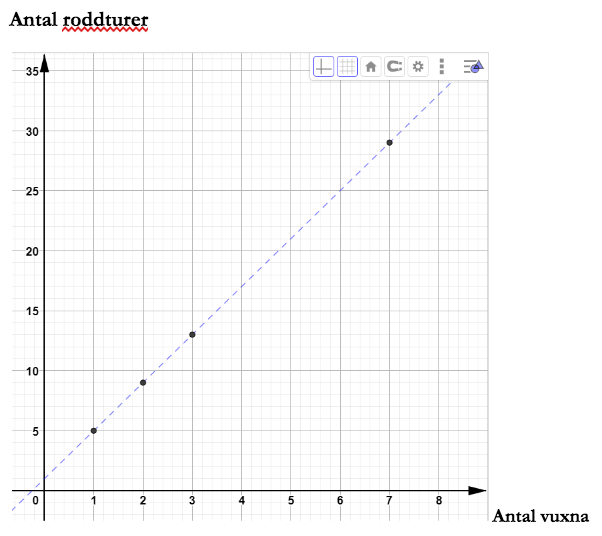
Algebraiskt uttryck:
(för n antal vuxna samt 2 barn)
n = antalet vuxna
4n+1
Vidareutveckling av uppgiften:
- Vad händer om där är ett annat antal vuxna? (För yngre barn kanske välja ett lägre antal vuxna till en början)
- Hur många var de totalt om antalet turer blev 129?
- Vad händer om där finns fler barn?
- Vad händer om de har ett annat antal båtar?
- Vad händer om där finns a vuxna, b antal barn och c antal båtar?
Länkar till dokument:
angelina.briggner
Sandra Johansson
Spara som favorit
Du måste logga in för att kunna spara som favorit.