Hur många svampar var det i korgen?

Om resursen

Målgrupp: 

Resursen är lämplig att användas på mellanstadiet, högstadiet eller kurs 1 på gymnasiet, beroende på vilket innehållsmål du har med lektionen (potenser och/eller binära tal).

Förbered: 

1. Det laborativa materialet. I varje laborationsgrupp ska det finnas 6 st (helst genomskinliga) plastmuggar, som fungerar som korgar, samt 63 stycken centikuber, eller annat laborativt material som kan symbolisera totala antalet svampar. Varje grupp ska ha en miniräknare som kan räkna med potenser.
2. Kopiera upp problemformuleringen på papper – en eller två exemplar per grupp.

Problemformuleringen: 

Sex gummor hade varit ute i skogen och plockat svamp. När de kom hem till stugan hällde de var och en ut alla svampar de plockat på bordet i köket. De räknade hur många där var tillsammans: 63 stycken.  Ert uppdrag är att ta reda på hur många svampar var och en hade plockat.

Ledtrådar:

• Alla har plockat minst en svamp.
• Ingen har plockat samma antal svampar.
• När du har rätt antal svampar i de sex korgarna, kommer du, genom att addera antalet svampar i olika kombinationer, kunna skapa alla heltal från 1  till och med 63.

Problemformulering.pdf

Problemformulering (lättare).pdf

3. Gruppindelning du anser är lämplig, max 4 elever per grupp.

Genomförande: 

Introduktionsfas: 

1. Dela in eleverna enligt den gruppindelning du förberett.
2. Presentera problemet för klassen genom att läsa upp problemet högt, gå sedan igenom problemformuleringen, så att alla har förstått vad problemet går ut på.
3. Dela ut problemformuleringen – en eller två exemplar per grupp.
4. Dela ut det laborativa materialet.

Problemlösningsfas:

Grupperna arbetar med att försöka lösa problemet max 20 minuter.

Om någon grupp hittar lösningen snabbt:        1       2        4       8       16        32

Ge gruppen några följdfrågor som kommer tas upp i den gemensamma genomgången sedan:

• Kan ni nu skapa alla tal från 1 – 63 med hjälp av antalet svampar i korgarna?
• Kan ni hitta något mönster i lösningen ni hittat?
• Kan ni skriva talen på något annat sätt?

Gemensam genomgång / klassdiskussion: Alternativ a – potenser

Frågor alternativ A.pdf

Ställ följande frågor till klassen: 

• Vilken lösning kom ni fram till? Skriv upp olika förslag till lösningar på tavlan. 
• Låt grupperna berätta sina lösningstrategier.
• Testa sedan de olika lösningarna genom att skapa alla tal från 1 – 63.

Undersök vidare:

• Kan ni se något mönster i de korrekta lösningarna?
• Kan man skriva om produkterna på ett smidigare sätt?
• Om ni tittar på talen i potensform. Hur skulle vi kunna skriva talet 1 som en potens med basen 2? Kan ni se något mönster?
• Uppmana eleverna att titta på den ursprungliga lösningen igen. Ni sa att det fördubblades – vilka tre tal borde stå före talet 1 om vi ska följa mönstret i talföljden?
• Hur kan vi skriva de här decimaltalen på ett annat sätt?
• Kan ni se något mönster i bråkens nämnare?
• Titta på talföljden som är skrivna i potensform? Om vi ska följa mönstret, hur skulle vi kunna skriva om talen 0,5, 0,25 och 0,125 som en potens med basen 2?

Sammanfatta därefter vad ni kommit fram till i klassdiskussion och presentera de nya potenslagarna:  

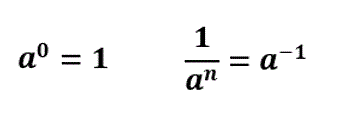
Gemensam genomgång / klassdiskussion: Alternativ b – binära talsystem

Frågor alternativ B.pdf

Om du genomfört alternativ A vid någon lektion, kan du hänvisa tillbaka till problemet och höra om någon kom ihåg lösningen till problemet när du ska introducera binära tal. Alternativt tvärtom. Om det är första gången genomför du introduktionsfas och problemlösningsfas som ovan.

1. Vilken lösning kom ni fram till? Skriv upp gruppernas förslag till lösningar på tavlan. 
2. Låt grupperna berätta sina lösningstrategier
3. Testa sedan de olika lösningarna genom att skapa alla tal från 1 – 63.

Ge klassen ett antal frågor att fundera över – be eleverna diskutera i par innan du ber något/några par delge sina tankar i helklass. Om olika svar be eleverna förklara sina tankar och försöka reda ut vad som är korrekt. Ge klassen en fråga i taget. 

1. Skriv upp lösningen på tavlan i fallande ordning, sudda ut övriga lösningar.                         32    16     8    4    2      1
2. Fråga eleverna: Vilka korgar använde ni för att till exempel skapa talet 5, 12 och 43?
3. Markera använda korgar som 1 och icke använda korgar som 0. De korgar som har högre värde och inte används får ingen siffra:
   

   	32	16	8	4	2	1
   Talet 5				1	0	1
   Talet 12			1	1	0	0
   Talet 43	1	0	1	0	1	1

4. Berätta för klassen att 101 är talet 5 skrivet i det binära talsystemet och talet 1100 är talet 12 skrivet i det binära talsystemet osv.

Att arbeta vidare med:

• Snabbare metod att skriva om med hjälp av multiplikation/division med rest. Hur skulle det se ut om vi hade ett talsystem som byggde på basen 3? Hur skulle till exempel talet 43 kunna se ut då?