Hur många kanonkulor finns det i pyramiden? är ett rikt matematiskt problem, som kan användas från senare delen på mellanstadiet ända upp till gymnasiet, beroende på hur djupt man vill dyka ner i problemet. Man kan återvända till problemet många gånger.
Grundproblemet handlar om ett antal kanonkulor som är staplade i form av en pyramid och man ska ta reda på antalet kanonkulor i bottenplattan när pyramiden är ett visst antal våningar hög. Sambandet eleverna kan upptäcka här är formeln för aritmetisk summa. I samband med detta kan man passa på att få in lite matematikhistoria och berätta om när lille Gauss överraskade sin matematiklärare. Att inleda med Gauss problem att summera alla tal från 1-100 är en bra ingång för mellanstadiet.
Ladda ner en pdf om det matematiska geniet Gauss.
Vill man ge eleverna en utmaning kan man be dem att försöka hitta fler vägar fram till lösningen och visa med hjälp av olika representationsformer. En riktig utmaning ger man om man utvecklar problemet vidare och tittar på totala antalet kanonkulor i pyramiden. Att arbeta med båda problemen ger ett ypperligt tillfälle för eleverna att i kurs 5 på gymnasiet att tillämpa sina kunskaper om talföljder och induktionsbevis.
Matematiken i problemet:
- Aritmetisk talföljd
- Aritmetisk summa
- Formel
- Rekursiv formel
- Tabell
- Funktion/graf
- Talmönster
- Ekvationssystem med fler än två obekanta
- Induktionsbevis
Gör så här!
Förbered:
- Dela in klassen i grupper om 3-4 elever per grupp. Bra om eleverna inte ligger alltför långt i från varandra kunskapsmässigt inom gruppen.
- Förbered eventuellt det laborativa materialet. Man kan använda centikuber, eller liknande som symboliserar kanonkulorna. Vill du att eleverna ska bygga pyramiden, kan du skapa delarna med hjälp av flirtkulor, som limmas ihop.
- Kopiera upp problemformuleringen (1-2 exemplar per grupp).
- Kopiera upp fyrfältaren, ett exemplar till varje elev.
Grundproblemet:
Ett antal kanonkulor är staplade som en pyramid.
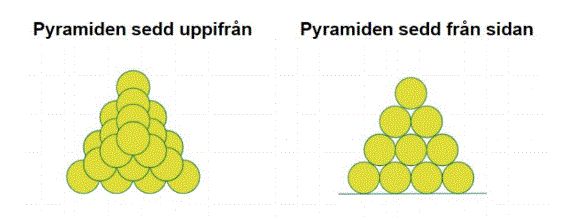
- Hur många kanonkulor finns det i bottenplattan på pyramiden som är 4 våningar hög?
- Hur många kanonkulor finns det i bottenplattan på en pyramid som är 6 våningar hög?
- Hur många kanonkulor finns det i bottenplattan på en pyramid som är 100 våningar hög?
- Hur många kanonkulor finns det i bottenplattan på en pyramid som är n våningar hög?
Vidare utmaningar:
- Hur många kanonkulor består hela pyramiden av om den är 4, 6, 100 respektive n våningar hög?
- Vad händer om bottenplattan istället är kvadratisk?
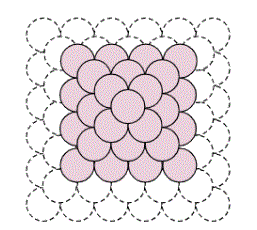
- Bevisa att formeln för totala antalet kulor i en pyramid är sann för alla heltal n≥1.
Arbeta med digitala verktyg och programmering:
Har man arbetat med problemet, kan man arbeta med programmering och digitala verktyg i någon anslutande lektion. Be eleverna skapa program för att beräkna antalet kanonkulor i bottenplattan och/eller för att beräkna totala antalet kanonkulor i hela pyramiden. Man kan också ge eleverna färdiga program, som de kan utveckla och förbättra. Ett annat alternativ är att arbeta med regressionsanalys i GeoGebra eller Googlekalkylark.
Nedanstående program är gjorda i Colaboratory, som är anpassat för Googlemiljön. Programmeringsövningen som ni hittar bland filerna nedan är också gjord i Colaboratory och det krävs att man lagt till appen i Google Drive för att kunna läsa filen.
Dokument:
Nedan hittar du en länklista med olika dokument kopplade till resursen.
Centralt innehåll matematik i grundskolan:
- Hur mönster i talföljder och geometriska mönster kan konstrueras, beskrivas och uttryckas (åk 4-6)
- Hur mönster i talföljder och geometriska mönster kan konstrueras, beskrivas och uttryckas generellt (åk 7-9)
- Strategier för problemlösning i vardagliga situationer och inom olika ämnesområden, samt värdering av valda strategier och metoder (åk 7-9)
- Hur algoritmer kan skapas, testas och förbättras vid programmering för matematisk problemlösning (åk 7-9)
Centralt innehåll matematik i gymnasieskolan (kurs 1 och kurs 5):
- Matematiska problem med anknytning till matematikens kulturhistoria (Matematik 1, 5)
- Strategier för matematisk problemlösning inklusive modellering av olika situationer, såväl med som utan digitala verktyg. (Matematik 1a, 1b)
- Strategier för matematisk problemlösning inklusive modellering av olika situationer, såväl med som utan digitala verktyg och programmering. (Matematik 1c, 5)
- Begreppen rekursion och talföljd (Matematik 5)
- Induktionsbevis med konkreta exempel från till exempel talteoriområdet. (Matematik 5)
Sandra Johansson
Spara som favorit
Du måste logga in för att kunna spara som favorit.